SigmaSTAT 4—统计分析软件

软件试用 获取报价

软件简介

SigmaStat 是一个易于使用、基于向导的统计软件包，旨在指导用户完成分析的每一步并执行强大的统计分析，而无需成为统计专家。SigmaStat 专为生命科学和医学研究领域量身定制，但对许多领域的科学家来说都是有价值的产品。

使用 SigmaStat，您可以确信您已正确分析数据。
您也可以节省时间！

因为它会带您逐步完成分析，SigmaStat 确保您：
• 使用正确的统计方法来分析您的数据
• 避免统计错误的风险
• 正确解释结果
• 生成适当的显示和专业报告

概述

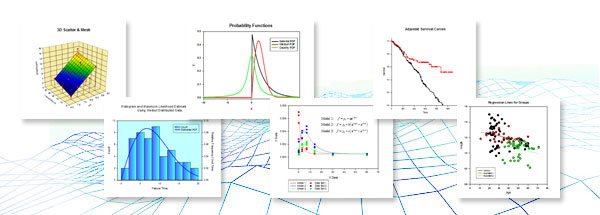
SigmaStat 提供了一系列功能强大且易于使用的统计分析，专为满足研究科学家和工程师的需求而设计。 借助程序中的功能，您将被引导完成选择合适的测试来分析数据、运行测试以及解释测试报告中的结果的过程。 对于许多测试，可以使用图表来总结测试结果。 程序中的编辑功能允许您自定义报告和图表的外观。您的最终结果可能会使用可用于导出的大量文件格式进行分发。

分析功能

回归向导

· 150 个内置拟合方程之一或用户定义的拟合方程求解非线性回归问题
· 可以使用多种数据格式从工作表中选择回归的原始数据，也可以从图中的图中选择
· 该程序的默认拟合库包含基于多项式、有理函数、指数增长和衰减、S 型函数、配体结合、波形、对数函数、概率分布和密度函数、分段线性等的模型
· 用户定义的方程是使用“编辑函数”对话框从回归向导创建的，并保存到我们的默认拟合库中。 可以选择保存到任何笔记本文件中。双击笔记本中的方程项将启动回归向导
· 拟合模型方程使用变换语言编码，可以包含常数、权重变量、线性等式和不等式约束以及其他变量的定义
· 算法所需的初始参数值可以指定为常数或使用我们在变换语言中的自动参数估计函数定义
· 拟合方程可以包含多达 500 个参数和多达 50 个自变量
· 加权回归支持定义为每个观察的常数或回归参数的函数的权重。权重函数允许用户应用稳健的程序进行参数估计，以减轻异常值的影响。程序的 fit 库和安装的示例文件中给出了示例
· 可用于创建回归报告或工作表中显示的多种类型的结果。
· 可以为具有两个或三个自变量的模型创建具有原始数据的最佳拟合方程图。可以添加置信区间
· 除了普通的数据拟合之外，还可以创建模型来解决其他类型的问题。 包括全局曲线拟合、求解方程组、分位数回归和分布拟合

直方图向导

· 生成工作表列的频率直​​方图
· 从多种图形输出样式中选择

绘制方程对话框

· 在二维或三维中创建函数图
· 输入用户定义的函数或从方程库中选择一个方程项
· 评估自变量的特定值的函数或求解方程以获得因变量的指定值的自变量的值。复制结果以粘贴到工作表、报告或图表页面

变换

· 在 User-Defined Transform 对话框中编写自己的称为 Transforms 的数值过程。转换语言提供了一个基于向量的计算环境，其中包含可以操作工作表数据并执行许多对数据分析很重要的计算的操作和函数
· 转换可以保存为笔记本文件中的项目，也可以保存为扩展名为 (.xfm) 的单独文件。安装的程序包含几个 (.xfm) 文件。这些变换中的计算过程示例包括累积分布函数、自举、峰值查找、频率表、D'Agostino-Pearson 正态性检验和估计随机变量函数的方差
· 变换语言用于绘制方程对话框和回归向导来定义笔记本中的方程项

快速变换

· 可以使用“快速变换”对话框快速创建和计算单线变换
· 该对话框支持列选择和功能调色板以轻松创建转换。
· 快速转换与他们用于输出的工作表一起保存
· 快速转换的输出可以根据输入数据的变化自动更新

典型图形

图表向导和直方图示例图表

统计特征

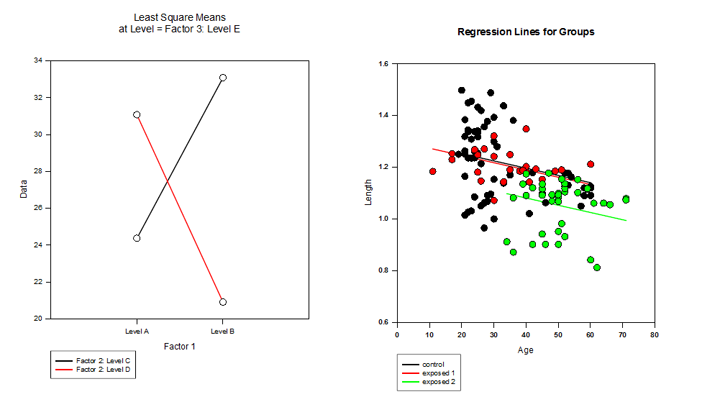
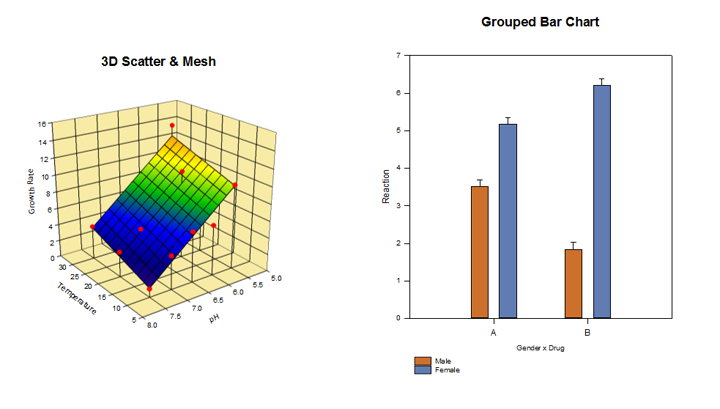
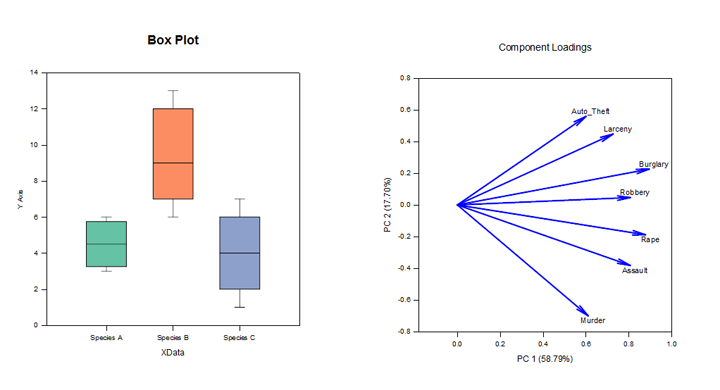
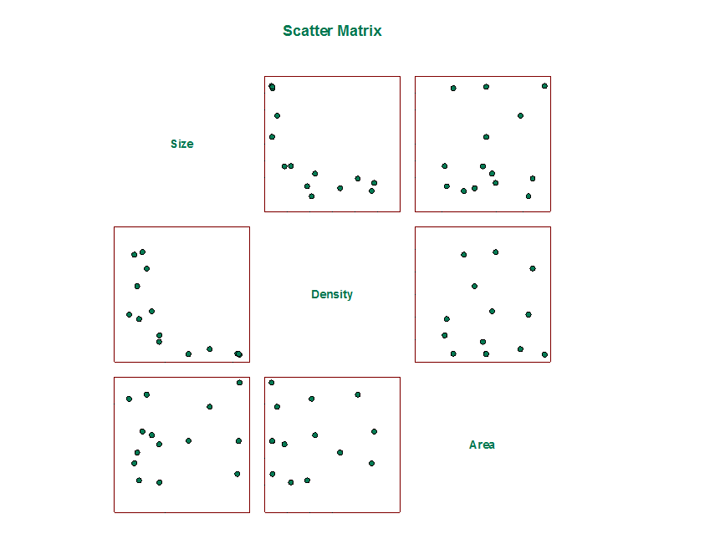
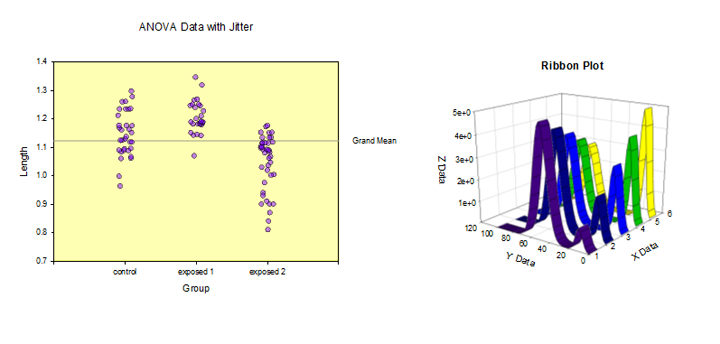
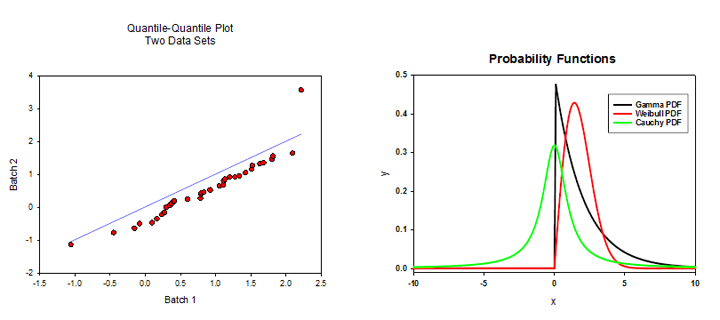
主成分分析 (PCA) – 主成分分析 是一种通过用较少维度逼近数据来降低高维数据复杂性的技术。每个新维度称为 主成分 ，表示原始变量的线性组合。第一个主成分尽可能多地解释数据的变化。每个后续的主成分尽可能多地解释剩余的变化，并且与所有先前的主成分正交。

您可以检查主成分以了解数据变化的来源。您还可以使用它们来形成预测模型。如果您的数据中的大部分变异存在于一个低维子集中，您可能能够根据主成分对响应变量进行建模。您可以使用主成分来减少回归、聚类和其他统计技术中的变量数量。主成分分析的主要目标是解释数据可变性的来源，并用较少的变量表示数据，同时保留大部分的总方差。

协方差分析 (ANCOVA) – 协方差 分析是通过将一个或多个协变量指定为模型中的附加变量而获得的方差分析的扩展。如果您使用 索引 数据格式在 SigmaPlot 工作表中排列 ANCOVA 数据，则一列将代表因子，一列将代表因变量（观察值），就像在 ANOVA 设计中一样。此外，每个协变量都有一列。

Akaike 信息标准 (AICc) – Akaike 信息标准已添加到回归向导和动态拟合向导报告以及报告选项对话框中。它提供了一种测量回归模型与给定数据集拟合的相对性能的方法。该标准基于信息熵的概念， 提供了使用模型描述数据时丢失的信息的相对度量。 更具体地说，它在最大化估计模型的可能性（与最小化残差平方和，如果数据是正态分布的）和保持模型中的自由参数数量最小化之间进行权衡，从而降低其复杂性。虽然拟合优度几乎总是通过添加更多参数来提高，但 过度拟合 会增加模型对输入数据变化的敏感性，并可能破坏其预测能力。 使用 AIC 的基本原因是作为模型选择的指南。在实践中，它是针对一组候选模型和给定数据集计算的。选择 AIC 值最小的模型作为集合中最能代表“真实”模型的模型，或者信息损失最小的模型，这就是 AIC 旨在估计的。 在确定了具有最小 AIC 的模型之后，还可以计算每个其他候选模型的相对似然度，以测量相对于具有最小 AIC 的模型减少信息丢失的概率。相对可能性可以帮助调查人员决定是否应保留集合中的多个模型以供进一步考虑。

非线性回归中的权重函数 – SigmaPlot 方程项有时使用权重变量来为回归数据集中的每个观察（或响应）分配权重。观测值的权重衡量其相对于抽样概率分布的不确定性。较大的权重表示观察值与其分布的真实平均值变化不大，而较小的权重表示观察值从分布的尾部采样得更多。 在使用最小二乘法估计拟合模型参数的统计假设下，在比例因子之前，权重等于对观测值进行抽样的（高斯）分布的总体方差的倒数。在这里，我们定义 残差，有时称为 原始残差，是在自变量的给定值下观察值与预测值（拟合模型的值）之间的差异。如果观测值的方差不完全相同（异方差），则需要一个权重变量，并 求解 最小化残差的加权平方和的加权最小二乘问题，以找到最佳拟合参数。