Stata车辆数据文件中车型的重量和油耗之间关系的对比和分析

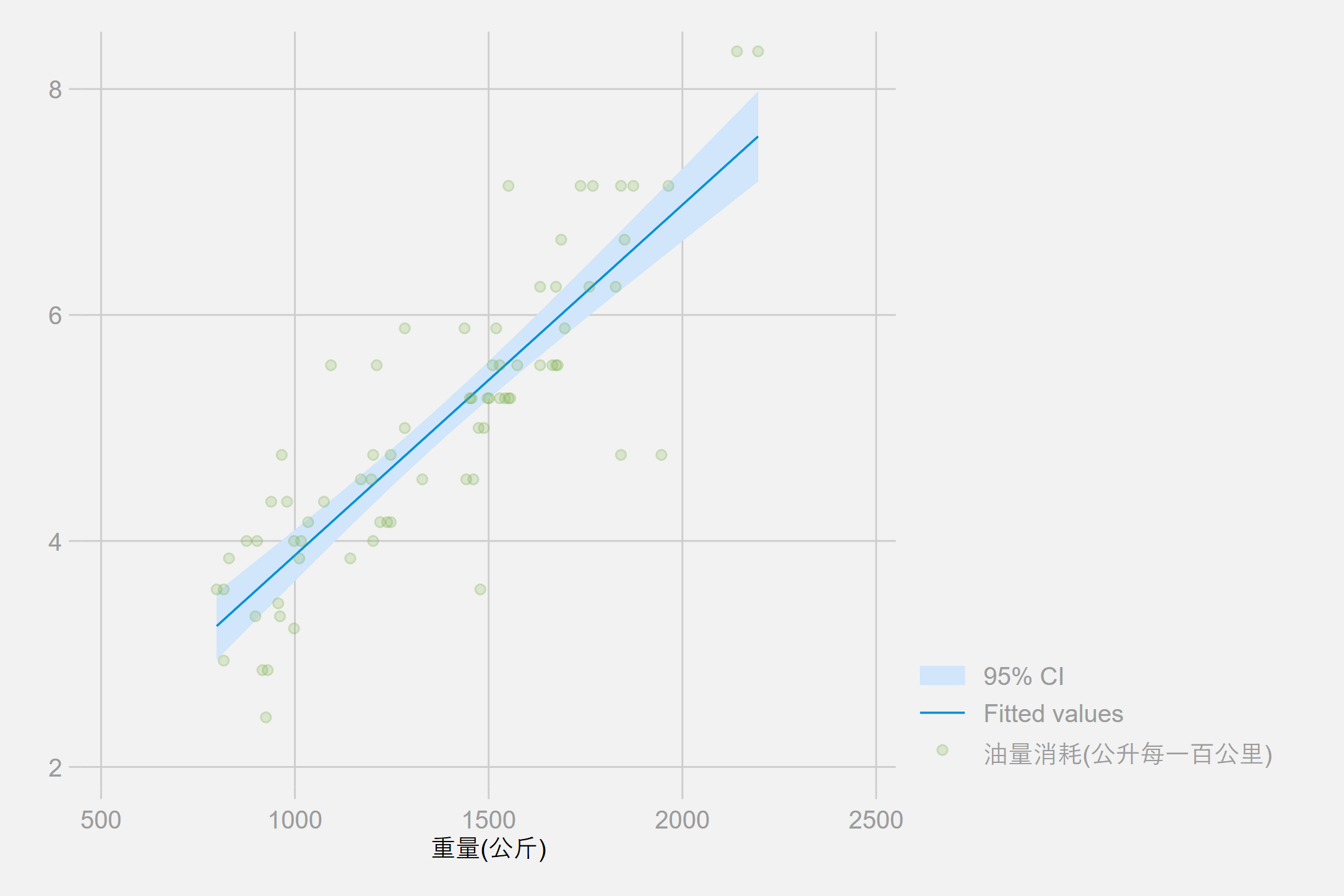
我们希望研究1978车辆数据中两个变量油耗和重量之间的关系。

. use auto_zh, clear

检查数据

首先我们检查油耗和重量的变量描述和摘要统计数据。

. describe 油耗 重量

              storage   display    value
variable name   type    format     label      variable label
--------------------------------------------------------------------------------
油耗            float   %9.0g                 油量消耗(公升每一百公里)
重量            float   %8.0gc                重量(公斤)


. summarize 油耗

    Variable |        Obs        Mean    Std. Dev.       Min        Max
-------------+---------------------------------------------------------
        油耗 |         74     5.01928    1.279856   2.439024   8.333333

从摘要统计数据看出，变量油耗的最小值2.44,最大值8.33,极差5.89。

. summarize 重量

    Variable |        Obs        Mean    Std. Dev.       Min        Max
-------------+---------------------------------------------------------
        重量 |         74    1369.603    352.5288   798.3219   2195.385

从摘要统计数据看出，变量重量的最小值798.32,最大值2195.39,极差1397.06。

用散点图显示油耗与重量关系

. twoway lfitci 油耗 重量 || scatter 油耗 重量, mcolor(%20) scheme(538)

油耗重量散点图

我们在油耗和重量的散点图上叠加拟合值与均值的置信区间。

用线性回归研究油耗与重量关系

. regress 油耗 重量

      Source |       SS           df       MS      Number of obs   =        74
-------------+----------------------------------   F(1, 72)        =    194.71
       Model |  87.2964971         1  87.2964971   Prob > F        =    0.0000
    Residual |  32.2797637        72  .448330051   R-squared       =    0.7300
-------------+----------------------------------   Adj R-squared   =    0.7263
       Total |  119.576261        73  1.63803097   Root MSE        =    .66957

------------------------------------------------------------------------------
        油耗 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        重量 |    .003102   .0002223    13.95   0.000     .0026589    .0035452
       _cons |   .7707669   .3142571     2.45   0.017     .1443069    1.397227
------------------------------------------------------------------------------

线性回归结果显示重量每增加一百公斤,每百公里油耗增加 0.3102公升, 可由模型解释的观察到的方差量为 73%.

用线性回归结果生成HTML表格

. _coef_table, markdown

油耗 Coef. Std. Err. t P>|t|[95% Conf. Interval]
重量 .003102 .0002223 13.95 0.000 .0026589 .0035452
_cons .7707669 .3142571 2.45 0.017 .1443069 1.397227

用estimates table生成表格

quietly regress 油耗 重量 变速比 转弯半径
estimates store 模型1
quietly regress 油耗 重量 变速比 转弯半径 国籍
estimates store  模型2
estimates table 模型1 模型2, b(%7.4f) stats(N r2_a) star

. estimates table 模型1 模型2, varlabel b(%7.4f) stats(N r2_a) star markdown

Variable 模型1 模型2
重量(公斤) 0.0030*** 0.0028***
变速比 0.1706 -0.3367
转弯半径(米) 0.0798 0.2010
国籍 0.8650***
Constant -0.5814 -0.4661
N 74 74
r2_a 0.7218 0.7637

legend: * p<0.05; ** p<0.01; *** p<0.001

用esttab生成表格

eststo : quietly regress 油耗 重量 变速比 转弯半径
eststo : quietly regress 油耗 重量 变速比 转弯半径 国籍
esttab using esttab_ex.html, label   /// 
	width(80%) nogaps                ///
	mtitles("模型1" "模型2")       ///
	title(线性回归结果)
线性回归结果
(1) (2)
模型1 模型2
重量(公斤) 0.00301*** 0.00278***
(6.09) (6.06)
变速比 0.171 -0.337
(0.64) (-1.19)
转弯半径(米) 0.0798 0.201
(0.70) (1.81)
国籍 0.865***
(3.66)
Constant -0.581 -0.466
(-0.38) (-0.33)
Observations 74 74
t statistics in parentheses
* p < 0.05, ** p < 0.01, *** p < 0.001

The community-contributed esttab is available on the Boston College Statistical Software Components (SSC) archive; see ssc install for details.